Para obter a certificação Black Belt é necessário adquirir um amplo conhecimento em Estatística. As teorias e ferramentas desta ciência são de grande importância em projetos Seis Sigma para que se possa obter informação dos dados gerando conhecimento sobre o processo. Nesse post abordaremos os principais conceitos de Probabilidade.
Probabilidade
A probabilidade é uma medida de incerteza e calculá-la permite compreender, qualificar e analisar variações que encontramos. Ela é utilizada para quantificar a possibilidade ou chance de ocorrência de um resultado de um experimento aleatório: “A chance de chover hoje é de 30%”, é uma afirmação que quantifica nosso sentimento acerca da possibilidade de chuva.
Um experimento é qualquer ação ou processo cujo resultado está sujeito à incerteza. A probabilidade está associada a experimentos aleatórios que tem como resultado um conjunto possíveis de resultados:
- Pagar uma conta: {Sim, Não};
- Tempo para completar uma ligação: {t: t>0};
- Número de cartões de crédito que um cliente possui: {1,2,3, …}
Cada resultado de um experimento aleatório é chamado de evento simples e a coleção de todos os eventos simples é denominado espaço amostral, podendo ser finito enumerável ou infinito não enumerável.
Distribuições de probabilidade
Uma função que atribui um número real a cada resultado do espaço amostral de um experimento aleatório é uma variável aleatória (v.a.), variável porque é possível obter diferentes valor numéricos e aleatória porque o valor observado depende de qual dos resultados possíveis do experimento é obtido. As variáveis aleatórias podem ser discretas ou contínuas:
- Variável aleatória discreta: Cujos valores possíveis constituem um conjunto finito ou infinito enumerável.
- Exemplo: Número de peças defeituosas e número de carros que passa por um pedágio em um determinado período de tempo.
- Variável aleatória contínua: Assume valores em um intervalo finito ou infinito de números reais.
- Exemplo: pH de um composto químico, altura, comprimento, peso e tempo.
A distribuição de probabilidade de uma variável aleatória (X) é uma descrição das probabilidades associadas com os valores possíveis de X. Por exemplo, um banco classifica seus clientes como “rentável”, “neutro” e “não rentável”, observando a seguinte proporção na base de clientes:

Definindo X a v.a. como : 1 – se o cliente é rentável, 0 se é neutro e -1 se é não rentável, temos como distribuição de X:
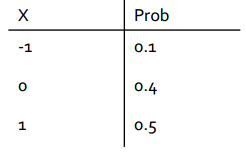
O conceito de variável aleatória e distribuição de probabilidade nos permite passar dos resultados do experimento propriamente ditos para uma função numérica dos resultados.
Para entender melhor este e mais conceitos de estatística confira nossos cursos de Green Belt e Black Belt. A EDTI possui conhecimento aprofundado sobre diversas ferramentas e estatística para melhorar sua empresa e se diferenciar no mercado.
Pingback: Como fazer o gráfico de CUSUM? | Escola EDTI - Acesse e Conheça nossos Cursos
Pingback: Correlação entre variáveis: Por que é importante entender? | Escola EDTI - Acesse e Conheça nossos Cursos