O que é Regressão Linear? Entenda aqui!

Você sabe como é feito um modelo de regressão linear? Esse nome ainda não é familiar? Pois bem, o conceito se refere a uma importante ferramenta da qualidade, capaz de cruzar dados de variáveis e fornecer importantes pistas para previsões de vendas, redução de erros estratégicos e tomadas de decisão mais precisas em diferentes operações.

Mas como isso pode ser útil nos processos da empresa? É simples! A regressão linear permite comparações de diversos fatores e, principalmente, do resultado delas. Então, o gestor consegue prever um valor de resposta para o seu projeto com muito mais precisão. Acompanhe o texto e descubra mais!

Afinal, o que é regressão linear?

Eu posso não ter muitas informações sobre você, leitor do nosso blog, mas se me disser sua altura, posso ter uma ideia do seu peso. Se me disser sua idade, posso lhe indicar uma música que provavelmente gostará. Se me disser sua escolaridade, posso ter uma estimativa de quanto você ganha por mês.

Pode parecer mágica, mas isso é apenas uma amostra do que é regressão linear. O método nada mais é do que estudar, em números, a relação entre variáveis. Você, com certeza, já visitou um site de compras e, ao clicar em um item, logo abaixo, encontrou a opção “Você provavelmente vai gostar desses outros produtos”.

Outro exemplo importante: se me disser qual foi o último filme que assistiu, posso lhe indicar um que com certeza gostará. É assim que funciona quando você vê um filme ou uma série na Netflix e, logo depois, ela lhe indica um outro título que surpreendentemente lhe agrada.

Isso são algoritmos que conseguem estimar o que você pode vir a gostar com base no que você já gostou ou visitou. Essa é a ideia central de uma regressão linear. Ou seja, estudar o que temos para poder entender como reagir no futuro. O método garante um aspecto importante no mercado hoje: a entrega de produtos cada vez mais customizados.

Como funciona, de fato?

Depois de ter uma ideia do que é o conceito por trás do método, trazendo para um cenário mais formal, fazer um modelo de regressão linear é estudar uma variável de interesse (variável dependente) em função de outras variáveis que me ajudarão a entendê-la — as chamadas covariáveis ou variáveis independentes.

Por exemplo, quero estudar como o preço do dólar se comporta em função da taxa de crescimento do Brasil, ou o exemplo clássico de tentar estimar o tamanho do pé de uma pessoa baseado em sua altura. Todos esses exemplos, tanto os acima como os do começo do texto, têm algo em comum: a relação entre as variáveis.

Essa relação pode ser estudada matematicamente, ou seja, podemos quantificar em números quanto uma variável está relacionada à outra e como ela impacta em seu comportamento. Para tanto, o primeiro passo é coletar dados. No modelo de regressão linear simples, temos duas variáveis:

• x: variável independente;
• y: variável dependente.

Para a interpretação da regressão linear, você pode criar um gráfico de dispersão ou utilizar o módulo de análise de dados disponível no Excel. A relação entre os fatores pode ser simples ou mais complexa. Quando se usa algo não linear para comparar as variáveis — como a raiz quadrada — ou mais que um fator preditor, estamos diante da regressão múltipla.

Matematicamente, o que é regressão linear?

Não queremos assustar ninguém demonstrando como funciona matematicamente, mas é bom termos uma noção do que uma regressão linear significa. No caso de duas variáveis, quando tenho dados de um par do tipo (x, y) e coloco em um gráfico, é possível observar aproximadamente como elas se comportam.

A regressão nos diz qual é a melhor curva a ser traçada e que se ajusta melhor nesses dados, podendo ser uma reta ou uma curva qualquer. Só de olhar para o gráfico, você já pode ter um palpite se é uma reta ou um polinômio de segundo grau, por exemplo.

O importante é que o método lhe diz qual é a melhor curva, de forma que a distância entre os pontos e a curva ajustada seja a menor possível. Ou seja, minimizo o erro e consigo estimar com maior precisão. Veja abaixo:

Exemplos

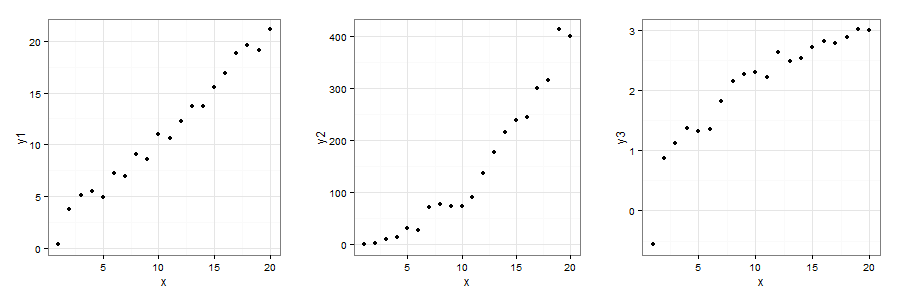
Para facilitar a compreensão, suponha que temos uma variável de interesse y e queremos estudar como ela se comporta em relação a x. Na figura acima, temos três exemplos, todos com 20 observações, ou seja, 20 pares de valores (x, y).

No primeiro gráfico, temos uma relação aparentemente linear, podendo ser uma reta a melhor curva, enquanto, nos outros dois casos, dificilmente uma reta se ajustaria bem. A lição aqui é verificar que, apesar de o nome ser regressão linear, temos mais opções além de traçar a melhor reta.

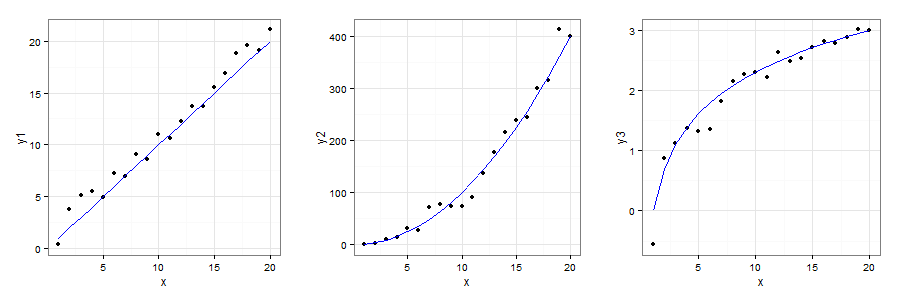
No primeiro caso, sim, temos que a melhor curva de ajuste é uma reta. Porém, no segundo, podemos supor que seja uma relação y = x^2, pois y cresce quadraticamente em relação a x. Já no terceiro gráfico, podemos supor que y = log (x), pois y tem o comportamento de uma função logarítmica. O resultado dos ajustes você pode conferir abaixo.

Mas regressão é o mesmo que correlação?

Há uma relação entre elas, mas não se confunda, não são a mesma coisa! A correlação é um número de -1 a 1 que nos diz o quanto duas variáveis estão relacionadas, sendo que, quanto mais próximo de 1, há a indicação de que quanto mais eu aumento uma, mais a outra também aumentará.

Por outro lado, quanto mais próximo de -1, há a indicação de que quanto mais eu aumento uma, mais eu diminuo a outra. Mas cuidado! Alta correlação não implica causalidade! Já escrevemos sobre isso e você pode conferir no nosso texto de planejamento de experimentos, basta clicar no link.

A relação entre correlação e regressão linear se dá pelo fato de que eu consigo construir uma boa regressão se minha variável de interesse e as variáveis independentes tiverem uma relação.

É só refletir: como você conseguiria estimar o preço do café baseado na nota média do ENEM? Ou como estimar o salário de alguém baseado em quanto tempo ele(a) consegue comer um cachorro quente? Não consegue, pois são variáveis sem relação alguma!

Do que eu preciso para fazer uma regressão linear?

Dados! Precisamos de dados de todas as variáveis envolvidas no processo. Apesar de termos mostrado apenas os exemplos de regressão linear simples, ou seja, o estudo da relação de apenas duas variáveis, podemos estudar a variável de interesse em função de várias variáveis independentes.

A ideia é que, quanto mais informação eu tenho acerca de um assunto, melhor eu posso falar sobre ele, certo? O mesmo funciona para esse método. Utilizando o modelo de regressão linear múltipla, isto é, com mais que uma única variável preditora, mais eu consigo explicar os resultados das combinações.

Como a regressão linear pode ser aplicada na minha empresa?

Se você gostaria de ter uma bola de cristal para adivinhar o futuro, a regressão linear deve ser uma boa solução para seus problemas. Ela serve para ficar de olho em possíveis cenários do negócio e, dessa forma, ser um importante suporte quantitativo para tomadas de decisão e apontamento de falhas. Veja!

Previsões de cenários

Como você já deve ter começado a assimilar, o modelo de regressão linear é uma técnica de previsão. Por meio do cruzamento matemático de dados, é possível analisar com uma boa margem de acerto o que provavelmente acontecerá no próximo bimestre, semestre ou ano na empresa.

Por isso, uma das principais utilidades do método é a previsão futura, que dispensa o “achismo” e baseia-se em indicadores concretos. Você consegue, por exemplo, estimar o aumento de impostos, as mudanças na economia local e a alteração no valor de gastos médio do seu consumidor.

Otimização de processos

Outra forma de usar o modelo de regressão linear é otimizando processos da empresa — tanto gerenciais quanto produtivos. Por exemplo, você pode elaborar um gráfico de comparação entre a estimativa do prazo de entrega de um produto indicada no site e o número de desistência dos consumidores na etapa do carrinho.

Dessa forma, você descobre que, ao ultrapassar certa quantidade de dias, o usuário costuma abandonar o site e, provavelmente, buscar por concorrentes com prazo menor. A ferramenta serve, portanto, para estudar a variabilidade de processos e as características que estão atrapalhando os resultados.

Tomadas de decisões

O modelo de regressão linear também ajuda a tomar decisões de apoio. Gestores e proprietários que buscam estabelecer uma posição competitiva no mercado não baseiam suas estratégias apenas em intuições ou achismos, mesmo que tenham bastante experiência no segmento.

A projeção de resultados a partir de dados permite que vários setores da empresa, como as áreas de finanças, compras e vendas, tenham iniciativas embasadas em previsões consistentes. As informações obtidas com a regressão linear, então, funcionam como um suporte empírico para as decisões gerenciais.

Quais são as vantagens que terei aplicando esse método?

As vantagens desse método estão na precisão de seus resultados. É comum que uma análise estatística tenha uma porcentagem representando a margem de erro. No entanto, ainda assim, as previsões são mais consistentes do que as análises de cenários puramente qualitativas.

Previsões mais precisas

Como você já viu, o uso consagrado da regressão linear dentro das empresas se refere à predição de situações. O modelo serve para prever eventos ou valores que ocorrerão futuramente, por isso, se construído com base em parâmetros estratégicos, proporciona importantes informações para a equipe gerencial.

Conhecer as diferentes possibilidades de futuro permite que, no presente, sejam realizadas alterações em processos ou mudanças no encaminhamento de planos de ação. Podemos dizer que a principal vantagem do método é fornecer terreno seguro para as iniciativas em diferentes projetos.

Correção de erros

Da mesma maneira que a regressão linear funciona para mostrar o melhor caminho para o processo, serve também para indicar o contrário, ou seja, as evidências de erros e falhas. Por isso, é uma importante aliada na correção de estratégias e do próprio pensamento gerencial.

Por exemplo, o gerente da filial sugere uma expansão da unidade pois acredita que o tamanho da instalação está diretamente relacionado à entrada de receitas. No modelo de regressão linear, no entanto, percebe-se que a proporção entre área física e vendas não compensa o aumento dos custos decorrentes da reforma, então, corrige-se a iniciativa antes de ocorrer um prejuízo.

Brainstorm

Por fim, outra grande vantagem dessa ferramenta é a otimização do brainstorm. Hoje em dia, os dados são a chave do sucesso de empreendimentos dos mais variados portes e nichos de atuação. Isso porque o perfil do consumidor mudou e exige entregas cada vez mais personalizadas e que vão ao encontro de suas reais necessidades.

Por isso, uma boa predição de comportamentos com base em parâmetros matemáticos ajuda a gerar novas ideias e insights para a gerência e as equipes de criação. Com as informações encontradas, são revelados padrões e relações que podiam, até mesmo, ser ignorados anteriormente.

Quando a regressão linear não é indicada?

A regressão linear depende da análise de dados coerentes. Por isso, ela não é indicada quando não se tem informações limpas e que façam sentido. Ou seja, se o modelo encontrar valores muito diferentes ou irreais, deve haver algo errado na construção da fórmula. Lembre-se de que, no campo matemático, um detalhe pode alterar completamente os resultados.

Após a leitura, você viu que o modelo de regressão linear é muito útil para gerir projetos com mais qualidade e eficiência. No entanto, o método deve ser sempre aplicado com muita coerência, pois construções ou interpretações equivocadas de dados matemáticos podem levar a decisões erradas.

Por isso, é importante ter muito conhecimento sobre o assunto. Que tal se aprofundar ainda mais? Clique e conheça nosso curso de Estatística e Análise de Dados!