Estudar a correlação entre variáveis é uma importante fonte para o entendimento de um problema e uma maneira de encontrar possíveis soluções. Quando estamos mapeando um processo de uma maneira macro precisamos identificar a saída do processo. Por exemplo, se estamos produzindo algum serviço, a saída é nosso serviço entregue, porém este serviço pode ser avaliado sobre importantes pontos de vista ou variáveis importantes para nosso cliente. A complexidade do serviço, por exemplo, quanto maior a complexidade maior o tempo de entrega ou talvez quanto mais mudanças maior o tempo de entrega.
A ideia é tentar encontrar alguma relação entre essas variáveis. Encontrando esta relação podemos encontrar uma maneira de melhorar o nosso processo.
Gráfico de dispersão e coeficiente de correlação
Quando medimos duas variáveis relacionadas a um mesmo problema, geralmente estamos interessados no estudo da relação entre as variáveis. Vamos considerar por hora a situação em que as duas variáveis podem ser consideradas como contínuas.
Exemplo. Uma empresa que distribui produtos por todo o país contrata uma empresa aérea para efetuar o transporte. Um estudo foi realizado pela empresa contratante para verificar a relação entre o custo de transporte (Y) e o peso do material transportado (X). Os dados se referem a um período de 6 meses e estão apresentados na tabela abaixo.
| Custo | Peso | Custo | Peso |
| 5492.29 | 3778.0 | 6143.24 | 4181.0 |
| 4401.89 | 3268.5 | 6309.65 | 4575.0 |
| 5721.46 | 4026.0 | 8391.60 | 6272.0 |
| 6237.14 | 4564.5 | 8530.49 | 6676.0 |
| 6396.44 | 4386.0 | 6343.74 | 4841.0 |
| 6863.91 | 5664.0 | 7482.64 | 6047.0 |
| 7258.21 | 4852.0 | 6467.10 | 5315.0 |
| 6643.56 | 5000.0 | 8768.30 | 6856.0 |
| 8515.98 | 6646.0 | 8833.71 | 7198.0 |
| 4687.63 | 3350.0 | 7987.36 | 6324.0 |
| 5928.33 | 3726.0 | 8267.05 | 6452.0 |
| 10856.09 | 8718.0 | 4829.24 | 3699.0 |
| 7766.47 | 5647.0 |
O primeiro passo na análise dos dados é colocar os pontos num gráfico cartesiano de Y em função de X.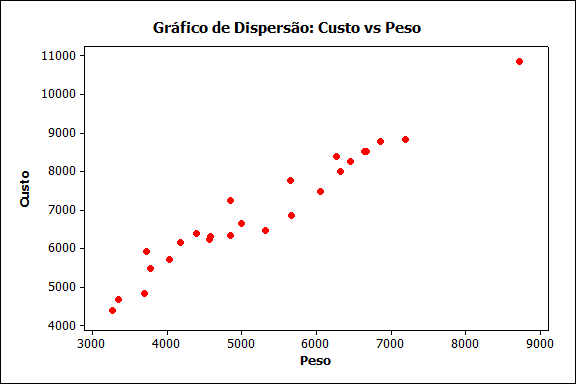
Do gráfico pode-se perceber que:
- Há uma tendência de aumento do custo com o aumento do peso (o que era de se esperar nesse exemplo)
- Que a relação entre as duas variáveis é aproximadamente linear na região em que temos observações
- Que há uma forte relação entre as duas variáveis.
Interpretação do coeficiente de correlação
O coeficiente de correlação mede a direção e o grau de associação linear entre as variáveis. Valores próximos de -1 ou +1 indicam forte associação. Valores próximos de zero indicam pouca associação. O sinal do coeficiente indica se a associação é positiva (Y aumenta com o aumento de X) ou negativa (Y decresce com o aumento de X).
O coeficiente de correlação para os dados acima é 0.98 e você pode calculá-lo com qualquer software de análise de dados, como o Excel.
Se os pontos no gráfico apresentam pouca dispersão em torno de uma reta ligando X e Y dizemos que existe uma forte correlação linear entre as variáveis. Se os pontos apresentam alta dispersão dizemos que as variáveis são pouco correlacionadas.
Uma forma de quantificar o grau de associação linear entre duas variáveis é através do coeficiente de correlação amostral. Ele mede o grau de associação linear que existe entre as duas variáveis.
Alguns exemplos de gráficos de dispersão
A seguir apresentamos diversas configuração de pares (X,Y)
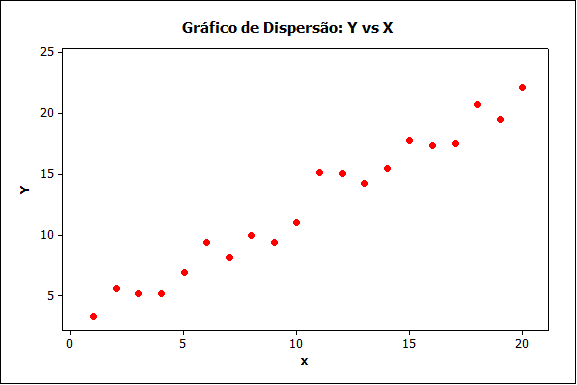
Figura (a)
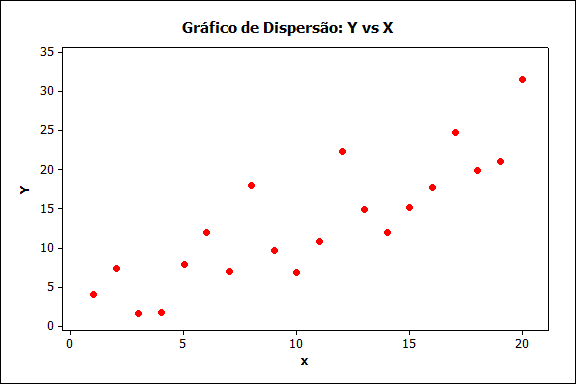
Figura (b)
Os diagramas da Figura (a) e (b) mostram duas situações onde os pontos estão em torno de uma reta imaginária ascendente. Valores pequenos de X estão associados a valores pequenos de Y, o mesmo acontecendo para valores grandes. Estes dois casos indicam o que chamamos de correlação linear positiva de Y e X. O dados em (b) estão mais próximos da reta imaginária, caracterizando uma correlação mais forte que a de (a), ou seja, o valor da correlação em (b) está mais próxima de +1 do que (a), apesar do que, os dois conjuntos de dados têm valor de r maiores do que zero.
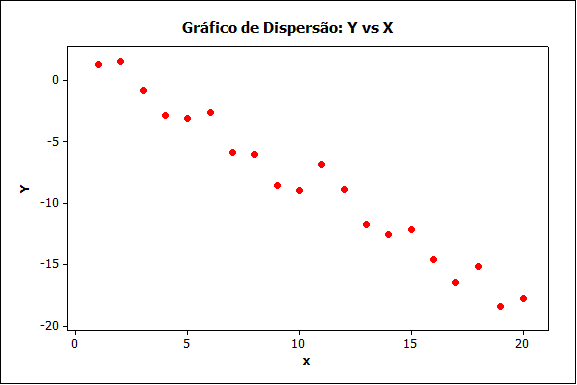
Figura (c)
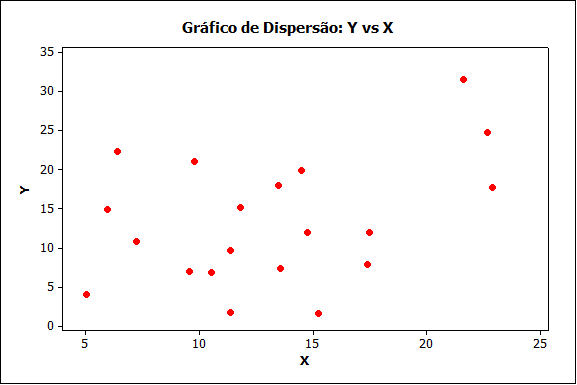
Figura (d)
A Figura (c) mostra que os pontos em X e Y estão em torno de uma reta imaginária descendente, indicando o que chamamos de correlação linear negativa, ou seja, valor de r menor que zero.
Os valores de X e Y na Figura (d) não sugerem uma associação entre duas variáveis pois valores pequenos, ou grandes, de X estão associados tanto a valores pequenos quanto a valores grandes de Y. Os pontos do diagrama não se posicionam em torno de uma linha imaginária ascendente ou descendente.
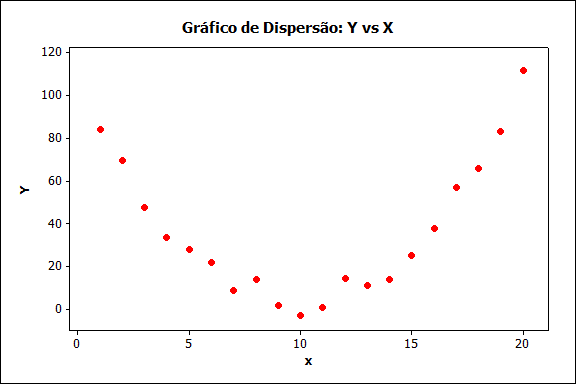
Figura (e)
A Figura (e) aproxima-se mais de uma parábola do que de uma reta, ilustrando correlação não linear. Apesar de serem muito correlacionados, o coeficiente de correlação linear será próximo de zero. Isto ocorre devido ao fato de que o coeficiente só pode ser usado para correlações lineares.
Aspectos importantes
Para começar o estudo de relação entre variáveis precisamos primeiro identificar alguns aspectos:
1. A variável é Y ou X?
- Y: Variáveis de saída do processo cujo comportamento você quer explicar e obter um modelo. Ela pode ser chamada de variável resposta ou variável dependente.
- X: Variáveis de processo ou de entrada, candidatas a explicar o comportamento das variáveis resposta. Podem ser chamadas de variáveis explicativas, variáveis independentes ou fatores.
2. A variável é numérica ou categórica?
Identificados estes aspectos basta localizar a técnica estatística adequada na tabela:
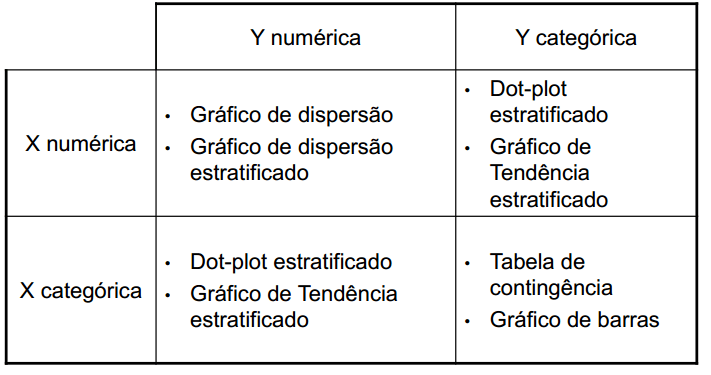
Exemplo: Associação entre variáveis X: numérica e Y: numérica
Uma equipe estava incumbida de elevar a satisfação dos clientes com a entrega dos projetos do escritório. Existia uma forte convicção de que a satisfação era influenciada pelos dias de atraso. Para comprovar essa teoria, a equipe coletou a satisfação e os dias de atraso (dias de atraso negativo significam entrega antes do prazo) para 24 projetos. Você consegue perceber se a satisfação é influenciada pelos dias de atraso com a entrega do projeto no gráfico de dispersão abaixo?
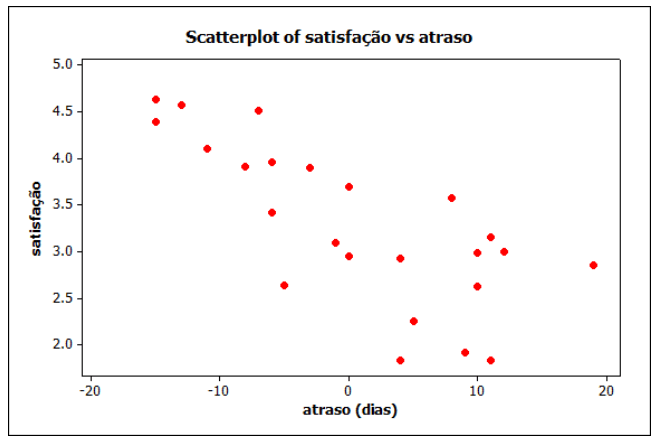
Olhando o gráfico de dispersão, onde cada ponto representa um projeto, com o respectivo atraso e satisfação, fica fácil perceber que quando maior o atraso, menor a satisfação.
Além do gráfico podemos também utilizar o Coeficiente de Correlação Linear que mede o grau de associação entre duas variáveis, este coeficiente pode ter valores entre -1 e 1 e quanto mais próximo de 1 maior a relação positiva e mais próxima de -1 maior a relação negativa entre as variáveis X e Y.
Correlação espúria: Cuidado!
Nem sempre correlação implica causalidade. Dizemos que uma variável X “causa” Y se X provoca um efeito ou resultado em Y. Devemos estar atentos para não confundir os conceitos de correlação e causalidade. Muitas vezes encontramos uma forte correlação entre duas variáveis e somos tentados a estabelecer uma relação de causa e efeito entre as duas variáveis, o que nem sempre é verdade.
Entre os anos 1920 e 1935 foram coletados os dados relativos ao número de aparelhos de rádio e número de doentes mentais por 100.000 habitantes na Inglaterra. O gráfico dispersão dos dados coletados esta na figura a seguir
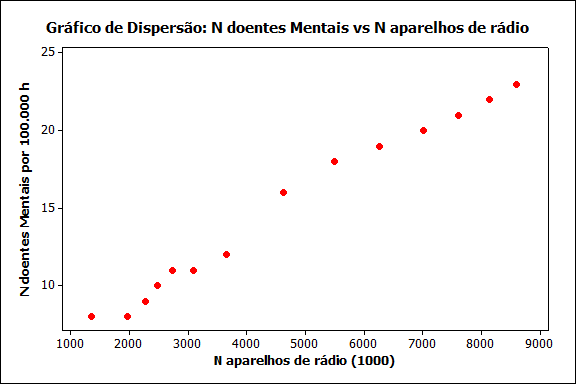
O gráfico sugere que quanto maior é o número de aparelhos de rádio, maior é o número de doentes mentais. Podemos concluir que ouvir rádio provoca doença mental?! A resposta é Não. Duas variáveis podem estar correlacionadas porque a variável X é causa direta da variável Y ou variável Y é causa direta da variável X; a variável X contribui para a variação em Y, mas não é a única causa; outras variáveis podem estar provocando a correlação; ambas as variáveis estão mudando com o tempo; a associação não passa de coincidência.
Quando encontramos uma correlação sem relação causal, dizemos que temos uma correlação espúria.
Relação de causa e efeito
Em muitas situações práticas não é tão simples decidir se a relação é causal. Uma forma de se estabelecer se a relação é de causa e efeito é através da realização de experimentos planejados.
Estudar a correlação entre duas ou mais variáveis pode ser bastante útil. Se Y é uma medida de um produto ou processo e se Y está fortemente correlacionada com outra medida X que é mais barata ou mais fácil de obter, então podemos medir X e através da relação existente entre elas estimar o valor de Y. A técnica utilizada nesse tipo de situação é regressão linear, que será estudada mais à frente.
Para saber mais sobre importantes ferramentas que auxiliam em projetos de melhoria, confira nossos cursos de Green Belt e Black Belt.
Bem apresentado!