Dossiê completo sobre análise de dados

Abordamos diversas vezes em nosso blog a importância da análise de dados. Hoje iremos postar um conteúdo completo sobre o assunto.

A análise de dados tem sido uma habilidade cada vez mais requisitada no mercado de trabalho. A quantidade de dados disponíveis é enorme, mas poucas pessoas conseguem transformá-los em insights para decisões de negócios.

Muitas vezes isso acontece porque as pessoas não sabem qual gráfico utilizar em cada uma das situações que lhes são apresentadas.

Pensando em ajudar você, na hora em que for realizar análises, a Escola EDTI montou este guia. Nele, você encontrará em linguagem simples e descomplicada a ocasião certa para utilizar cada tipo de gráfico, como interpretar os resultados e exemplos para ajudá-lo nas aplicações práticas.

Você saberá “quando” e “como” usar os seguintes gráficos: histograma, boxplot, gráfico de dispersão (correlação), gráfico de Pareto e gráfico de tendência.

Também incluímos uma seção introdutória para você preparar melhor sua análise e aumentar ainda mais a
qualidade dos seus resultados.

Este material é para ser utilizado como um guia de bolso e ajudá-lo a melhorar suas decisões e apresentações gráficas. Use e abuse!

Como é feita uma boa análise de dados?

Comece pelas pergunta

Antes de mais nada, é preciso ter perguntas! O que queremos responder? Quais são os pontos nebulosos em nossa estratégia de negócios? O que tem gerado muita discussão e poderia ser clareado com os dados?

Esse será o ponto de partida para uma análise rica. Nesse momento, quanto mais conhecimento sobre o problema, mais relevantes serão as questões propostas. Caso você não seja um expert no assunto em análise, procure quem seja para ajudá-lo a preparar perguntas relevantes.

Invista um bom tempo nessa preparação inicial. Não fique afoito para partir direto para a análise. Uma boa reflexão nessa etapa é um investimento que fará você ganhar muita qualidade analítica em seus estudos.

Descubra onde e como os dados serão obtidos

Com as dúvidas iniciais em mãos, é preciso levantar os dados necessários para respondê-las. Eles já estão disponíveis? Se sim, em qual sistema e quem terá que extrair essas informações? Os dados disponíveis são confiáveis?

Essa fase de questionamento é relevante. Afinal, caso os dados sejam ruins, a análise gerada também será. Portanto, a preocupação com a qualidade dos dados é de vital importância.

Tome especial cuidado para que todos os dados necessários para responder às perguntas sejam solicitados ou coletados, para evitar perder tempo nas próximas etapas.

Organize os dados em uma estrutura de banco de dados, com variáveis nas colunas e observações nas linhas, uma vez que a maioria dos softwares de análise exige essa organização.

Execute a análise

Comece avaliando a presença de outliers e investigue a razão da ocorrência desses valores atípicos ou discrepantes.
Caso eles existam, o que você fará? Eles realmente fazem parte da população em estudo ou são erros de digitação?
Essa é uma fase que nos ajuda a fazer uma limpeza dos dados, deixando-os prontos para a análise.

Com os dados preparados para a análise, comece respondendo às perguntas iniciais. Para cada gráfico preparado,
anote os aprendizados. Lembre-se de que a análise é iterativa, ou seja, as respostas às perguntas iniciais levam à
formulação de novas perguntas e esse ciclo segue-se diversas vezes.

Faça um compilado com os principais gráficos e resultados. Discuta com outras pessoas. Veja se aparecem novas
dúvidas e volte à análise.

Lembre-se de que a qualidade visual é importante, assim, faça ajustes nos eixos e legendas dos gráficos para que esses fiquem claros e visíveis para sua audiência, mas cuidado para não rebuscar demais, evitando que as conclusões sejam de difícil compreensão – quanto menos tinta melhor!

É importante pontuar que é preciso desenvolver a habilidade de interpretação gráfica. É possível fazer um paralelo
com médicos que se especializam em interpretar exames como ressonância magnética.

Para uma pessoa que não foi treinada, provavelmente seja impossível entender esse tipo de informação. Com os gráficos também é preciso treino e, por essa razão, colocamos as nossas interpretações em cada gráfico dos exemplos, para ajudá-lo a desenvolver essa habilidade.

Conceitos iniciais para suportar uma boa análise de dados

Estatística, Análise de Dados e Variabilidade

A Estatística é um conjunto de conceitos e técnicas, utilizado no planejamento da coleta e na análise de dados, com
o objetivo de resolver problemas reais.

Claramente, cientistas, engenheiros, economistas e outros profissionais estão envolvidos com essas atividades e, portanto, necessitam utilizar a Estatística. Além disso, de uma forma ou de outra, todas as pessoas são afetadas pelo uso da Estatística.

Cada vez mais órgãos governamentais e empresas baseiam as próprias decisões, as quais afetam o dia a dia das pessoas, em análises estatísticas, o que faz com que não apenas profissionais tenham de adquirir algum conhecimento dessa técnica.

O que torna essa disciplina de grande utilidade, e única, é que a aplicação dela ocorre em situações ou processos em que a incerteza e a variabilidade estão presentes.

Um processo é definido como uma combinação de pessoas, materiais, procedimentos, métodos, políticas e meio
ambiente, cujos elementos integrados formam uma série de ações que conduzem a determinado resultado.

Em nosso caso, o resultado é um produto ou serviço. Para avaliar a utilidade de um produto para o consumidor, variáveis são medidas no produto.

Dois itens produzidos nas mesmas condições não são, em geral, idênticos, com respeito às variáveis consideradas. Existe uma variabilidade inerente em cada processo.

Os métodos estatísticos são desenvolvidos para lidar com a incerteza e a variabilidade. Eles são fundamentais para se fazer inferências sobre processos a partir de uma amostra de uma população.

Considere, em seguida, exemplos de algumas áreas de atividade.
• Processos econômicos: renda familiar, índice de inflação, taxa de juro etc.
• Processos industriais: porcentagem de peças defeituosas, diâmetro de peças, rendimento de um processo industrial etc.
• Processos biológicos: pressão arterial, número de espécies, tempo de vida etc.

Em todas as situações descritas anteriormente, o que obtemos são respostas, as quais podem assumir diferentes características: podem ser resultados numéricos (renda familiar, tempo de sobrevivência) ou simplesmente resultados qualitativos (opção partidária, local de nascimento, sobrevivência ou não de um animal etc.).

Para avaliar a performance do processo e a qualidade do que se está produzindo, é preciso dados sobre o processo ou
o produto.

Os dados devem ser analisados, e as decisões devem ser feitas com respeito ao processo, além de que elas
devem ser tomadas na presença de variabilidade. A Estatística é a ferramenta adequada para se planejar a coleta de
dados, que sejam relevantes para o problema em estudo, bem como para a análise.

Tipos de dados

Antes de realizar qualquer análise, é preciso entender qual o tipo de dado que está na sua frente. Quando queremos
colocar um prego na parede utilizamos um martelo, já quando queremos apertar um parafuso podemos usar uma
chave de fenda.

Da mesma forma, dependendo do tipo de variável que coletamos, iremos utilizar uma ferramenta gráfica diferente. Em termos gerais, os dados podem ser de três tipos, como você pode observar a seguir.

• Classificação (qualitativos): os resultados possíveis são classificações (peça defeituosa ou não defeituosa,
entrega atrasada ou não atrasada, cliente satisfeito ou não satisfeito, cor de determinado produto);
• Contagem: os resultados são números inteiros (número de riscos em uma peça, número de acidentes no mês,
número de cursos vendidos);
• Contínuos: os resultados podem ser quaisquer números dentro de um intervalo (peso, comprimento, gasto mensal).

Quando, como e exemplos para gráficos:

Com esses conceitos em mente, confira em seguida nossas dicas para você construir e analisar gráficos.

Histograma

Histograma é uma representação gráfica da distribuição de frequências de um conjunto de dados quantitativos contínuo, pode ser um gráfico por valores absolutos ou frequência relativa ou densidade.

Em termos matemáticos, um histograma é uma função que conta o número de observações de cada um dos intervalos de classe. Um gráfico é apenas uma forma de representar um histograma.

Então, se for o número total de observações e se for o número total de intervalos de classe, o histograma satisfaz a seguinte condição:

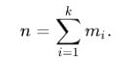
Quando utilizar: adequada para quando temos dados numéricos e desejamos aprender sobre a distribuição dele.

No caso de densidade, a frequência relativa do intervalo i, (fri), é representada pela área de um retângulo que é colocado acima do ponto médio da classe i.

Consequentemente, a área total do histograma (igual a soma das áreas de todos os retângulos) será igual a 1. Assim, ao construir o histograma, cada retângulo deverá ter área proporcional à frequência relativa (ou à frequência absoluta, o que é indiferente) correspondente.

Já para os onde os intervalos são de tamanhos (amplitudes) iguais, as alturas dos retângulos serão iguais às frequências relativas (ou iguais às frequências absolutas) dos intervalos correspondentes.

Como interpretar: no histograma olhamos informações de localização e de variação dos dados. Por exemplo, qual o centro (a média), qual o mínimo e o máximo, qual a amplitude (variação)?

O objetivo é conhecer um pouco sobre os dados que estamos trabalhando e também identificar a possível presença de outliers.

Por essas razões, o histograma é uma das primeiras ferramentas que utilizamos na chamada análise descritiva ou exploratória de dados.

Geralmente se recomenda a utilização de histogramas de frequência relativa, pois a influência do tamanho da amostra é minimizada, tornando possível comparar duas distribuições.

A utilização do histograma depende do tipo de variável coletadas e que será utilizada:

• Classificação (qualitativos): os resultados possíveis são classificações. No contexto de indicadores aparecerão na forma sim ou não (peça defeituosa ou não defeituosa, entrega atrasada ou não atrasada, cliente satisfeito ou não satisfeito).
• Contagem: os resultados são números inteiros (número de riscos em uma peça, número de acidentes no mês).
• Contínuos: os resultados podem ser quaisquer números dentro de um intervalo (peso, comprimento, gasto mensal).

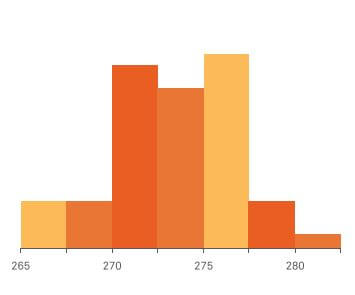
Exemplo: 60 registros do peso de uma caixa de leite em pó foram coletados durante uma hora de produção.
A distribuição é representada graficamente pela figura ao lado.

Por meio do gráfico podemos observar o comportamento dos pesos e examinar características como: simetria da distribuição (nesse caso distribuição simétrica), região onde há maior concentração de valores (entre 270 e 277), o centro da distribuição (em torno de 273), a dispersão dos valores ao redor de uma medida central (dados entre 265 e 283). Também é possível perceber que não existe nenhum outlier.

A distribuição nos fornece uma grande quantidade de informações sobre o conjunto de dados que estamos analisando, além de ser um bom estudo inicial, que nos permite ganhar mais familiaridade com a variável em estudo.

Boxplot

O boxplot (gráfico de caixa) é um gráfico utilizado para avaliar a distribuição empírica do dados. O boxplot é formado pelo primeiro e terceiro quartil e pela mediana.

As hastes inferiores e superiores se estendem, respectivamente, do quartil inferior até o menor valor não inferior ao limite inferior e do quartil superior até o maior valor não superior ao limite superior. Os limites são calculados da forma abaixo:

Para este caso, os pontos fora destes limites são considerados valores discrepantes (outliers) e são denotados por asterisco (*). O boxplot pode ainda ser utilizado para uma comparação visual entre dois ou mais grupos. Por exemplo, duas ou mais caixas são colocadas lado a lado e se compara a variabilidade entre elas, a mediana e assim por diante. Outro ponto importante é a diferença entre os quartis que é uma medida da variabilidade dos dados.

Quando utilizar: assim como o histograma, o Boxplot (também chamado de box e whisker plot) também é utilizado para variáveis numéricas, quando o objetivo for o estudo da distribuição dos dados, é um método alternativo ao histograma para representar os dados, preferível quando o objetivo é comparar dois ou mais grupos.

Em um box plot são apresentados 5 estatísticas: o mínimo, o primeiro quartil (Q1), a mediana, o terceiro quartil (Q3) e o máximo. Esse valores também são chamados de resumo dos cinco números.

Como interpretar: o Boxplot fornece informação sobre as seguintes características do conjunto de dados: localização, dispersão, assimetria, comprimento da cauda e outliers (medidas discrepantes). O centro da distribuição é indicado pela linha da mediana, no centro da caixa.

A dispersão é representada pela amplitude do gráfico, que pode ser calculada como máximo valor – mínimo valor. Quanto maior for a amplitude, maior a variação nos dados.

Exemplo 1: Na figura, a seguir, você encontra todas as informações apresentadas em um Boxplot.

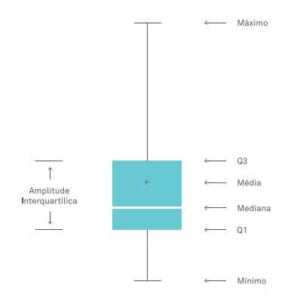
O centro da distribuição é indicado pela linha da mediana (alguns softwares estatísticos também representam a média com um símbolo, nesse caso o ‘+’).

A dispersão é representada pela altura do retângulo (Q3 – Q1), no qual Q3 é o terceiro quartil e Q1 é o primeiro quartil. O retângulo contém 50% dos valores do conjunto de dados.

A posição da linha mediana no retângulo informa sobre a assimetria da distribuição. Uma distribuição simétrica teria a mediana no centro do retângulo, bem próxima à média – no exemplo anterior, o conjunto de dados foi assimétrico.

Se a mediana é próxima de Q1, então, os dados são positivamente assimétricos. Se a mediana é próxima de Q3, os dados são negativamente assimétricos.

O comprimento das linhas fora do retângulo (algumas vezes chamadas de whisquers) informam sobre a cauda da distribuição.

Os valores fora de Q1-1.5*(Q3-Q1) e Q3+1.5*(Q3 -Q1) geralmente são chamados de outside e devem ser investigados como possíveis outliers, além de serem geralmente representados por um asterisco.

Valores outside não são necessariamente outliers, mas um outlier usualmente aparece no gráfico como um outside.

Uma utilidade muito importante do Boxplot é na comparação gráfica de dois ou mais grupos. Nesse caso, o Boxplot é
preferível ao histograma. Essa comparação pode ser feita desenhando-se os Boxplots para cada conjunto de dados,
paralelamente, em um mesmo gráfico.

Exemplo 2: O próximo gráfico apresenta dados de viscosidade de três misturas diferentes. O Boxplot comparativo é apresentado abaixo.

Como podemos ver, as misturas apresentam níveis médios diferentes de viscosidade, decrescentes da mistura 1 para a mistura 3.

Supondo que no exemplo o desejo seja aumentar a viscosidade, claramente a mistura 1 é preferível nesse critério.

Também é possível perceber que existe razoável simetria nos dados para as 3 misturas e que para a mistura 3 existe um outlier (representado pelo ponto isolado no gráfico).

Esse ponto deve ser investigado, e causa dele, identificada. É importante ressaltar que muitas vezes a grande informação está na causa especial, por isso, não a ignore simplesmente.

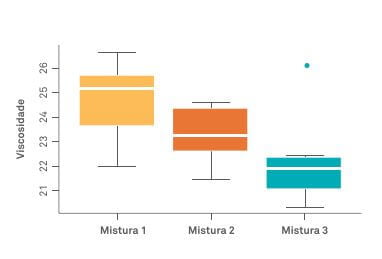
Gráfico de dispersão

Quando utilizar: quando queremos estudar a relação entre duas variáveis numéricas. O objetivo é responder à pergunta: a variável X influencia a variável Y?

Se conseguirmos entender como ocorre a relação entre as variáveis, pode ser possível propor novos direcionamentos para um negócio.

Por exemplo, podemos descobrir que o tempo para responder a uma proposta influencia negativamente a chance de sucesso na venda e, com isso, redesenhar as atividades da área comercial de modo a diminuir esse tempo de envio de propostas.

Como interpretar:

• Direção: positiva (quando “x” aumenta e “y” também aumenta) ou negativa (quando “x”
aumenta e “y” diminui);
• Forma: a relação é linear (pode ser aproximada por uma reta) ou não linear;
• Força: quanto mais aproximados os pontos estão da forma da relação identificada entre “x” e “y”, maior a força dessa relação.

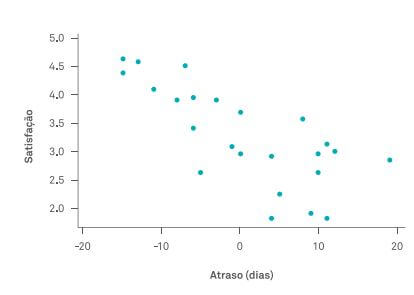
Exemplo: Uma equipe estava incumbida de elevar a satisfação dos clientes com a entrega dos projetos do escritório. Existia uma forte convicção de que a satisfação era influenciada pelos dias de atraso.

Para comprovar essa teoria, a equipe coletou o nível de satisfação e os dias de atraso (dias de atraso negativos significam entrega antes do prazo) de 24 projetos.

Você consegue perceber, no gráfico de dispersão, acima, se a satisfação é influenciada pelos dias de atraso da entrega do projeto? Olhando o gráfico de dispersão, no qual cada ponto representa um projeto, com os respectivos atraso e satisfação, fica fácil perceber que, quanto maior o atraso, menor a satisfação.

Além do gráfico, podemos também utilizar o Coeficiente de Correlação Linear, que mede o grau de associação entre
duas variáveis. Esse coeficiente pode ter valores entre -1 e 1.

Quanto mais próximo de 1 ele estiver, maior será a relação positiva, e quanto mais próximo de -1, maior a relação negativa entre as variáveis X e Y.

Cuidado especial deve ser tomado em relação a possíveis relações espúrias ou “viciadas”.

Gráfico de Pareto

Quando utilizar: quando queremos representar a distribuição de dados categóricos e ordená-los por frequência. Muitas vezes essa forma de representação gráfica é utilizada para focar esforços, localizando quais são as categoriais vitais de uma realidade, para atuação posterior.

Como interpretar: quando o gráfico é construído de maneira adequada, é calculada uma linha que identifica os percentuais acumulados (veja exemplo a seguir).

As categoriais vitais são definidas quando o crescimento de uma barra para outra se estabiliza. É importante perceber que nem sempre o efeito de Pareto está presente, não indicando nenhuma grupo de categoria vital.

Exemplo: Uma empresa de embalagens precisava reduzir custos com peças defeituosas encontradas em sua produção.

Como a empresa não sabia por onde começar, decidiu-se utilizar o conceito do Gráfico de Pareto para analisar quais
defeitos ocorriam com maior frequência. Durante duas semanas os dados foram coletados, resultando no gráfico ao lado.

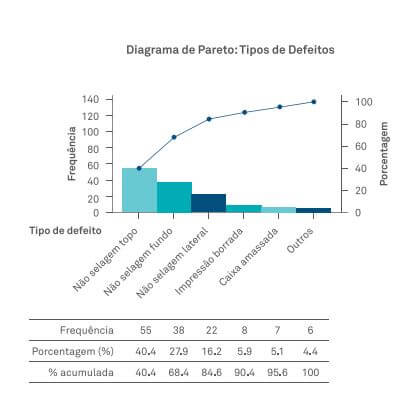
Nesse caso, a análise do gráfico de Pareto permitiu à empresa identificar quais eram os defeitos mais recorrentes
e, assim, priorizar a solução dos problemas relacionados à não selagem do topo, não selagem do fundo e não
selagem lateral.

Vamos utilizar esse exemplo para entender como encontrar as categorias vitais. Para isso, observe a linha azul, que mostra o percentual acumulado.

Perceba, no exemplo analisado, que da primeira para a segunda barra acontece um grande salto. Da segunda para a terceira barra também ocorre um grande salto. A partir da terceira barra os saltos ficam quase do mesmo tamanho e, com isso, podemos concluir que encontramos as categorias vitais: as representadas pelas três primeiras barras.

Gráfico de tendência

Quando utilizar: quando o objetivo é avaliar o comportamento de um indicador ao longo do tempo. Pode ser utilizado para variáveis numéricas ou classificatória, nesse segundo caso é preciso calcular o indicador na escala percentual, para posterior utilização no gráfico de tendência.

Como interpretar: o grande objetivo é avaliar o comportamento ao longo do tempo (estabilidade), além da presença de causas especiais de variação que mereçam uma ação pontual ou o impacto de mudanças no indicador.

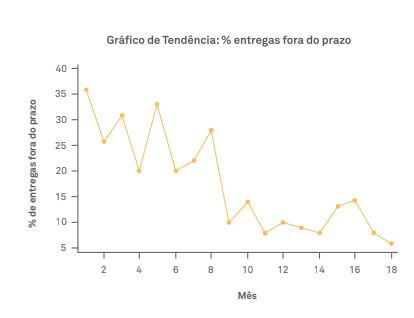
Exemplo 1: a figura, abaixo, é um exemplo de um gráfico de tendências que mostra o percentual de entregas fora do
prazo (observação: essa é uma variável classificatória – fora ou dentro do prazo – em que foi calculado um percentual ao longo do tempo para acompanhamento em um gráfico de tendência).

É fácil perceber, pelo gráfico, que houve uma melhoria no indicador entre os meses 8 e 9, causando redução no percentual de entregas atrasadas.

Uma questão importante é quando temos convicção de que a melhoria realmente aconteceu e se sustentou.

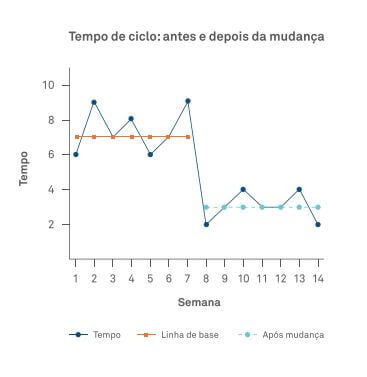
Exemplo 2: Em um Gráfico de Tendência é útil criar “fases” no gráfico para evidenciar osimpactos produzidos por mudanças. No exemplo, a seguir, o objetivo era reduzir o tempo de ciclo de uma atividade, e uma mudança foi realizada entre a semana 7 e 8.

Claramente podemos verificar que a mudança produziu o efeito desejado. Observe.

Uma dúvida recorrente, especialmente de pessoas que estão iniciando a utilização de gráficos de tendência para monitorar  indicadores, é quando criar “fases” em um Gráfico de Tendência.

Essa é uma pergunta sempre complicada principalmente quando estamos reagindo a posteriori (após “ver” os dados), ou seja, já temos dados do indicador que cobrem um período anterior às mudanças, o período em que mudanças foram realizadas e um período após a implementação das mudanças (fase de controle).

A situação ideal é a que denominamos “análise prospectiva”. Quando iniciamos um projeto, coletamos dados do
indicador de um período anterior (em geral em torno de 10 pontos é suficiente).

Colocamos esses pontos em um Gráfico de Tendência e tentamos avaliar se não há evidência para rejeitar que o indicador estava estável no período (atenção para o detalhe: “se não há evidência para rejeitar” e não “se há evidência para aceitar” – é sútil).

Se não há evidência para rejeitar que o indicador estava estável, então, traçamos a linha de base e a projetamos para o futuro.

A partir disso começamos a colocar novos pontos no gráfico e anotamos mudanças que são realizadas no processo. Se a regra de 8 ou mais pontos acima ou abaixo da linha de base é satisfeita, então, criamos uma nova linha de base
com esses novos pontos.

Se conseguimos associar a mudança de linha de base com alguma mudança realizada de forma intencional no
processo, ótimo.

Se não conseguimos associar a alteração na linha de base com alguma mudança feita de modo intencional, então, devemos tentar identificar alguma transformação que foi executada, às vezes sem nosso conhecimento, que possa explicar esse impacto no indicador.

E assim prosseguimos acompanhando o processo, alterando a linha de base quando o indicador mostra que algo mudou no processo que impactou o indicador.

Exemplo de como definir fases em um gráfico de tendência.

No exemplo anterior, a sequência seria a que você pode ver em seguida. Acompanhe.

1) Medimos o tempo de ciclo por sete semanas, antes de se fazer mudanças no processo, e construímos um Gráfico de Tendência com os dados. Não há indicação de que o indicador não esteja estável.

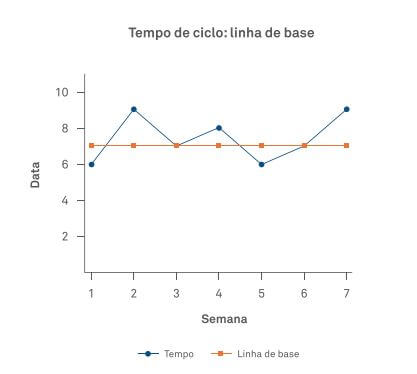
2) Projetamos a linha de base.

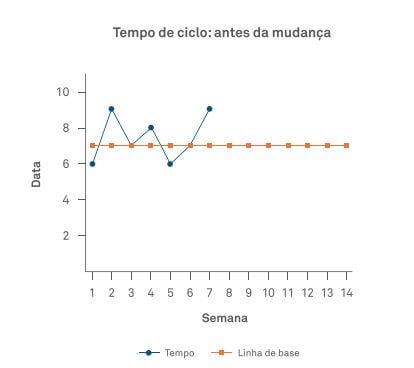
3) Coletamos pontos após a mudança e colocamo-nos no Gráfico de Tendência.

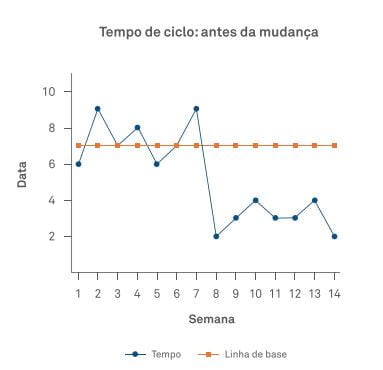
4) Após a mudança (realizada entre a sétima e a oitava semana), há sete pontos abaixo da linha de base. Então, é o
momento de alterar a linha de base.

O valor 3 para o tempo de ciclo (mediana dos últimos sete pontos) é a nossa referência agora. Os dados mostram que a mudança foi uma melhoria.

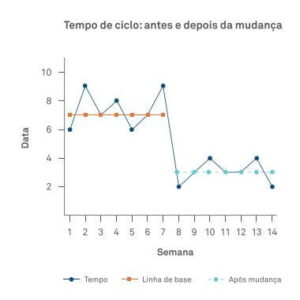
Percebemos que uma correta análise de dados auxilia nos direcionamentos estratégicos das decisões que devem ser
tomadas diariamente nas organizações.

Para que você tenha sucesso e insights valiosos é necessária uma preparação adequada, levantando perguntas que direcionarão a construção de gráficos.

Para responder às perguntas propostas será necessário o conhecimento e entendimento de quais gráficos são
adequados para cada pergunta e para cada variável, como descrito no decorrer desse dossiê.

A constante análise gráfica e fundamentação de suas decisões em dados e informações pode ser o diferencial entre você e seus concorrentes.

Bons resultados!