Você já ouviu falar do Diagrama de Venn?
A ferramenta, cuja origem está na Matemática, tem sido de grande auxílio dentro da gestão de negócios e de produção por oferecer uma visualização facilitada de dados em um gráfico.
Ela funciona como um eficiente sistema para organização de conjuntos de elementos, dispondo e arranjando os diferentes valores em grupos de acordo com suas características.
Para tanto, o diagrama separa as informações em dois ou mais grupos, representando os números totais e parciais de cada um, além de revelar o valor que resulta da intersecção deles e da união de todos.
Se este é o seu primeiro contato com a ferramenta, tudo isso pode parecer um pouco confuso – o que é natural.
Mas, acredite, a lista de benefícios trazida pela aplicação do Diagrama de Venn é extensa, começando pela sua simplicidade.
Ele torna mais fácil a tarefa de organizar os dados de forma visual dentro de um sistema sucinto e, assim, é capaz de ordenar e transmitir diversas informações de uma só vez.
Outra vantagem é que a ferramenta permite a comparação rápida entre duas ou mais escolhas, usando o raciocínio lógico na tomada de decisão e na resolução de gargalos na produção antes que eles levem a prejuízos.
Dentro da indústria, essa é uma solução que pode também ser usada em circuitos digitais, facilitando a representação de funções lógicas.
Todas as razões para usar o Diagrama de Venn serão detalhadas neste artigo, que também vai avançar quanto ao seu significado e funcionamento.
Ao final da leitura, você não só vai entender o que a ferramenta é, como dominar suas aplicações e aprender como desenvolver um sistema para ajudar no dia a dia da produção.
Interessado? Então, vamos começar!
O que é o Diagrama de Venn?
Chamamos de Diagrama de Venn os gráficos utilizados dentro da Matemática para expressar características de diferentes conjuntos e, a partir disso, resolver problemas e tomar decisões sobre o manejo das informações disponíveis.
Ainda que seja bastante aplicado nos dias de hoje, a origem do método é antiga, datando do século XIX.
O diagrama foi originalmente criado pelo matemático e filósofo inglês John Venn (1834-1923), que introduziu essa parte do seu legado pela primeira vez em julho de 1880, em publicação na Philosophical Magazine and Journal of Science.
Seu trabalho representa uma continuação do que vinha sendo estudado por filósofos desde a Alemanha, com Gottfried Leibniz, e de volta ao Reino Unido, com George Boole e Augustus de Morgan.
Prova disso é que, inicialmente, o próprio autor denominou seu trabalho como Círculos Eulerianos, uma referência aos diagramas propostos pelo suíço Leonhard Euler no século anterior.
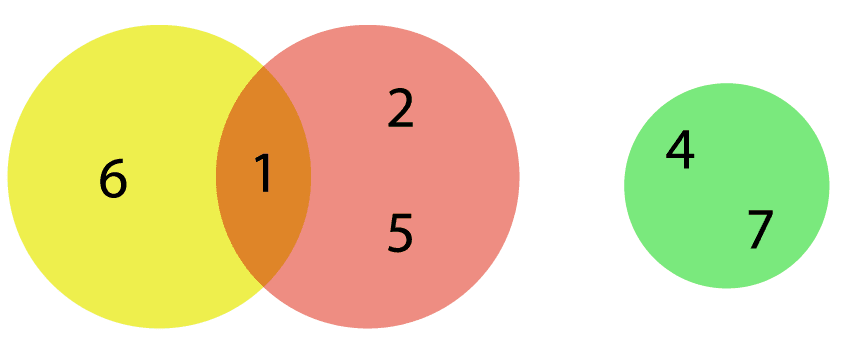
O Diagrama de Venn é constituído por círculos dispostos sobre um plano, com curvas fechadas simples, onde são representadas as informações que pertencem a determinado conjunto.
Cada círculo representa, então, uma categoria. E os elementos que se assemelham serão agrupados dentro de um mesmo conjunto – um dos círculos desenhados no eixo.
Ainda, os elos representados podem se sobrepor um ao outro – se o contexto das informações permitir. E o resultado do encontro entre duas ou mais figuras é chamado de intersecção.
Esse espaço é reservado para os elementos que são comuns a ambos conjuntos, ou seja, informações que pertencem a mais de uma categoria.
O resultado da soma de todos os valores representados nos conjuntos do diagrama é chamado de união.
Na imagem que você observa acima, é possível identificar todos esses elementos.
Mas para que não restem dúvidas sobre eles, vamos detalhar melhor cada um deles no próximo tópico.
Quais são os Elementos do Diagrama de Venn (Glossário)
O Diagrama de Venn conta com diversos elementos, tanto para sua construção quanto para análise de resultados.
Confira abaixo os principais termos envolvidos no uso da ferramenta e seus significados:
- Conjunto: assim chamamos a coleção de elementos consideradas dentro do sistema. O diagrama é extremamente versátil e, por isso, permite que os conjuntos sirvam para agrupar diferentes informações, como produtos, objetos, processos, pessoas e funções
- União: assim é chamada a soma de todos os elementos expressos nos diferentes conjuntos de um diagrama. A união de dois conjuntos (A e B) é expressa pela fórmula A U B
- Intersecção: dois conjuntos podem ter semelhanças entre si, e o nome dado para os elementos comuns entre eles é intersecção. Para expressar os elementos que se repetem entre dois (A e B) ou mais conjuntos, utilizamos a fórmula A ∩ B
- Complemento absoluto: é chamado assim o agrupamento de todos os elementos que se encontram em um conjunto (A), inclusive aqueles que são comuns aos outros conjuntos. Esse valor é representado por Ac
- Complemento relativo: termo que diz respeito aos elementos que constam em um conjunto (A), mas não estão em outro conjunto (B). Para simbolizar o complemento relativo, usamos a fórmula A ∩ Bc = A / B
- Teoria dos Conjuntos: é assim denominado o ramo da matemática inaugurado ainda durante o século V a.C., e aperfeiçoado por John Venn. A Teoria dos Conjuntos se dedica ao estudo das relações entre diferentes conjuntos. Extrapolando o mundo dos cálculos, o tema tem sido aplicado com sucesso também na gestão dos processos de produção
- Notações de conjuntos: as relações explicitadas pelo Diagrama de Venn podem ser descritas usando uma série de notações gráficas, algumas delas já apresentadas acima, como nos casos de intersecção (∩), união (U) e complementos (Bc)
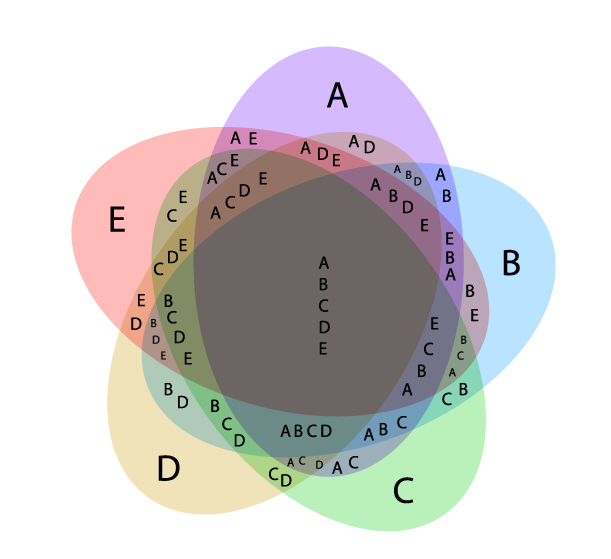
- Triângulo Reuleaux: assim é chamado o caso em que um diagrama conta com três eixos circulares, formando quatro intersecções específicas. O nome vem do seu inventor, o cientista e engenheiro alemão Franz Reuleaux. Para que o triângulo se caracterize, é preciso que o diagrama tenha três intersecções de dois conjuntos cada, e uma intersecção maior ao centro englobando os três conjuntos do sistema
- Diagrama Venn dimensionado: os conjuntos nem sempre são representados com as mesmas dimensões. No caso do Diagrama Venn dimensionado, eles têm tamanho proporcional à quantidade de elementos neles representada. Esse método de expor os dados é, por vezes, chamado também de área proporcional
- Diferença simétrica de dois conjuntos: por fim, este termo diz respeito à união dos elementos presentes em todos os conjuntos, menos os valores expressos na intersecção.
Vantagens e Benefícios do Diagrama de Venn
O Diagrama de Venn tem diversas vantagens e benefícios que servem de argumento para a sua aplicação nas mais diversas áreas.
O primeiro e talvez mais óbvio item da lista é a facilidade que ele proporciona para uma análise dos dados dentro de um sistema.
Com a representação gráfica, é possível categorizar itens de acordo com suas semelhanças e diferenças, registrando as informações de forma sistemática e sintética para uma melhor visualização do cenário completo.
Assim, auxilia ao pensar sobre a lógica que está por trás de um conceito, por exemplo.
Nesse sentido, pode ser usado também para ajudar a entender o funcionamento de equações e de declarações complexas.
Ainda dentro da Matemática, o método funciona muito bem para simplificar a resolução de problemas e axiomas difíceis de serem finalizados.
Ele também pode ser usado por gestores como um suporte a mais para avaliar as opções dentro de um processo decisório.
Afinal, ao representar todas as informações de forma gráfica, fica mais fácil visualizar os possíveis desdobramentos de cada escolha e agir preventivamente.
Esse processo pode ser implementado, por exemplo, na escolha de fornecedores e na análise de aceitação de mercado dos produtos desenvolvidos.
Aplicação do Diagrama de Venn na Indústria (Circuitos Digitais)
As aplicações do Diagrama Venn dentro do contexto industrial surgem de um paralelo com a álgebra booleana.
Esse campo de estudos da Matemática foi proposto pelo cientista que deu seu nome, o já mencionado britânico George Boole.
A obra The Mathematical Analysis of Logic, publicada em 1847, introduz os primeiros conceitos que viriam a ser a lógica simbólica ao propor, pela primeira vez, que era possível usar equações algébricas para representar questões lógicas.
Boole comprovou ser possível pensar em uma outra aplicação da álgebra comum, partindo de circuitos construídos pela combinação de portas lógicas.
Assim nasceu a álgebra boolena, com a diferença fundamental de que, aqui, as variáveis e funções podem ter apenas valores 0 e 1.
Esses valores são resultado das portas lógicas, que bifurcam sempre o fluxo de informação e cujo resultado será sempre por um lado ou outro.
Essa lógica binária foi a base para o desenvolvimento da informática e é aplicada até os dias de hoje na construção de Circuitos Digitais.
Neste contexto, o Diagrama de Venn pode ser usado para expressar graficamente os resultados de qualquer equação, fragmentado os circuitos para entender o funcionamento geral do sistema.
Outros Diagramas similares
É verdade que o Diagrama de Venn não está isolado como única ferramenta matemática que pode ser utilizada na gestão da produção, quando traduzida para o mundo dos negócios.
A lista de diagramas matemáticos, obviamente, é muito extensa. Por isso, separamos abaixo apenas os quatro mais relevantes dentro do contexto corporativo.
Alguns dos exemplos são, inclusive, anteriores ao grafismo proposto por Venn.
A álgebra booleana surge como lugar comum, ainda que o raciocínio que levou a invenção de alguns deles parta de outros campos de estudo da lógica que não a matemática.
Diagramas de Euler
Este é um dos diagramas similares ao Venn que antecedem à sua criação.
Ainda que sua representação gráfica seja muito parecida visualmente, os Diagramas de Euler se diferem do de Venn pelo fato de que a intersecção nem sempre acontece ou precisa acontecer.
A representação é visualmente mais simples, já que os conjuntos avaliados podem não ser intrínsecos.
Seu objetivo principal é representar um universo de discurso onde as relações entre conjuntos nem sempre são possíveis ou necessárias.
Para facilitar o seu entendimento, podemos pegar um exemplo da biologia: os mamíferos são animais, mas nem todo animal estará dentro do conjunto dos mamíferos – ainda que todos mamíferos estejam dentro do conjunto de animais.
Paralelo a isso, uma bromélia está dentro desse universo, mas representa um conjunto próprio e separado do conjunto de animais – as plantas.
Nesse caso, não haverá intersecção, pois é impossível que um ser vivo seja ao mesmo tempo animal e planta – ainda que animais e plantas estejam dentro de um mesmo universo de discurso.
Diagrama de Johnston
O Diagrama de Johnston tem uma representação quase idêntica àquela utilizada por Venn, mas não se engane: cada um deles funciona de uma forma distinta.
A principal diferença de Johnston é que, em sua representação, ele mostra proposições e suas operações lógicas, em vez de elementos arranjados em conjuntos.
Aqui, estamos falando muito mais de sentenças lógicas propriamente do que da classificação de objetos ou itens dentro de um sistema.

Podemos dizer que essa é uma ferramenta mais voltada para o planejamento do que para avaliar resultados.
Para entender melhor, vamos considerar que estamos trabalhando com dois círculos, que representam as sentenças lógicas A e B.
De acordo com Johnston, a partir dessa representação gráfica, podemos interpretar que a intersecção entre os dois grupos representa a sentença A e B.
Ainda, a união é representada pela sentença A ou B e o conjunto complementar é representado como nem A nem B.
Mapa de Karnaugh
Também conhecido como Diagrama de Veitch, o Mapa de Karnaugh é um dos diagramas similares que deriva da lógica proposta pela álgebra booleana.
Este método de simplificação gráfica é mais recente, tendo sido desenvolvido na década de 1950 pelo matemático estadunidense Edward Veitch e, posteriormente, aperfeiçoado por seu conterrâneo, o engenheiro Maurice Karnaugh.
Ele é representado por um mapeamento biunívoco, desenvolvido a partir dos valores representados em uma tabela verdade da função.
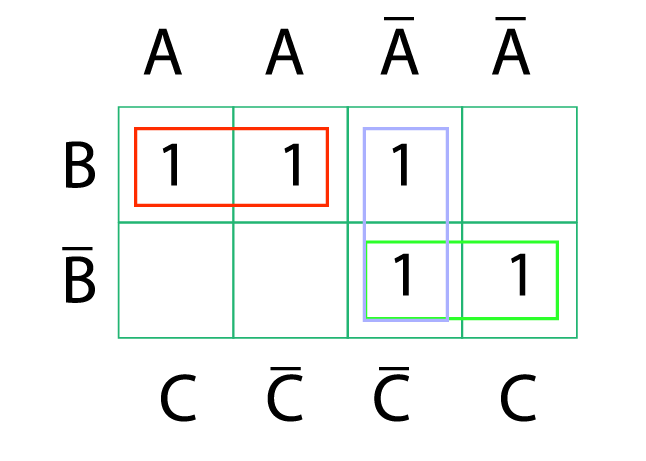
Nessa tabela, são dispostos de maneira visual os produtos que são fundamentais para a resolução de um problema.
De certa forma, o método é considerado mais simples, pois elimina o erro das simplificações, comum a outros usos da lógica booleana.
Ele sempre funciona apenas com dois valores de entrada e resultado (0 e 1), e existem diversos modelos prontos que podem ser aplicados conforme sua necessidade.
Diagrama de Peirce
Este último exemplo funciona como um complemento ao Diagrama de Venn.
O nome vem seu criador, o matemático e filósofo estadunidense Charles Peirce, da Universidade de Harvard.
Peirce ficou mais conhecido, porém, por suas contribuições no campo da filosofia, sendo o fundador do Pragmatismo e da ciência dos signos, a Semiótica.
De volta ao campo da Matemática, o autor cria seu diagrama depois de verificar que, dentro do Venn, seria impossível expressar outros tipos de objetos sintáticos que representariam um comprometimento existencial.
Ele precisava de um grafismo capaz de representar sentenças existenciais, disjuntivas e de probabilidade, entre outras.
Assim, nasce o Diagrama de Peirce como uma extensão do conhecimento acumulado na área até então.
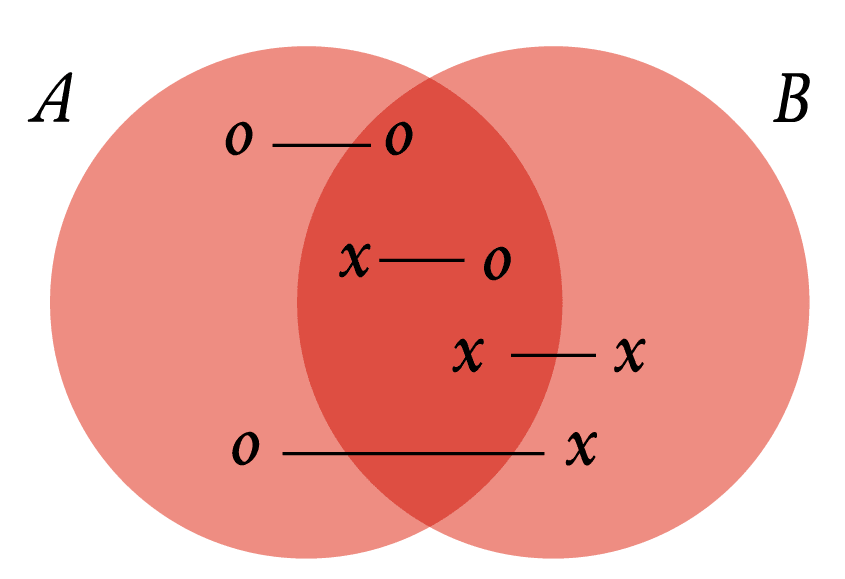
Entre suas contribuições e adaptações, estão a substituição da coloração utilizada por Venn pelo símbolo “o”, a inclusão de “x” para representar os valores de informação disjuntiva, além da proposição de linhas para expressar as relações entre “o” e “x”.
Como Fazer um Diagrama de Venn
A construção de um Diagrama de Venn não tem nenhum mistério. Afinal, sua principal proposta é apresentar as informações de maneira simplificada.
Tudo começa com a definição do seu objetivo.
Então, pergunte-se qual universo será representado e qual análise deverá decorrer da representação gráfica.
Realizadas essas definições, você precisa relacionar os elementos que serão representados.
Dentro de ambientes corporativos, é importante chamar o restante da equipe para participar desta etapa, promovendo um brainstorming coletivo para garantir que nenhum elemento será esquecido.
O último passo é colocar a mão na massa e começar a elaborar seu diagrama de acordo com as informações que foram levantadas.
Se estiver trabalhando com poucos conjuntos, você pode desenhar os círculos primeiro e preencher com os elementos posteriormente.
No caso de diagramas que contam com três ou mais conjuntos, talvez valha a pena registrar primeiro as relações entre os grupos e, só então, partir para a representação gráfica.
Exemplos Práticos para Uso na Empresa
Apesar de essa ser uma ferramenta que parte do mundo da Matemática, ela é largamente aplicada na gestão de empresas dos mais diversos segmentos.
É uma metodologia que facilita a tomada de decisão como um todo e, por isso, tem o grande potencial de facilitar o dia a dia do gestor.
Uma de suas aplicações se dá na representação de estatísticas para uma análise comparativa.
Com os dados dispostos de maneira visual, fica muito mais fácil decidir estrategicamente e agir de maneira preventiva – evitando gastos inesperados com manutenção corretiva, insumos e recursos humanos.
Esse último setor, inclusive, pode se beneficiar especialmente do Diagrama de Venn com sua aplicação em processos seletivos.
O método pode ser ainda utilizado por engenheiros de produção para verificarem a viabilidade de um produto, ilustrando uma comparação das características e da rentabilidade de maneira prática.
Extremamente versátil, o Venn se faz muito eficaz dentro de empresas, podendo ser adaptado para inúmeras funções.
Conclusão
Foi-se o tempo em que o uso do Diagrama de Venn ficava restrito às aulas de Matemática.
A ferramenta, capaz de organizar elementos em conjuntos e representar suas relações, caiu nas graças de empresas de forma geral.
Sua representação simplificada dos dados é capaz de comunicar várias informações ao mesmo tempo, de maneira organizada.
Por isso, o método se tornou aliado de gestores para comparar diferentes produtos ou serviços e tomar a decisão mais assertiva com base nos dados.
Experimente aplicar a metodologia em sua empresa e observe os benefícios de uma gestão que tem a lógica como aliada na tomada de decisões.
Se o artigo foi útil, compartilhe! E aproveite também para deixar seu comentário sobre o tema.