Afinal, de onde vem os 3,4 PPMs do Six Sigma?
Uma questão muito comum em cursos de Lean Six-Sigma é a respeito de como calcular os 3.4 referentes a um processo Seis-Sigma. Na estatística a letra sigma é utilizada para designar o desvio padrão, um valor que nos diz quanto de variabilidade existe em um processo.
Para continuar a responder essa pergunta podemos olhar para a figura 1. Nela temos a distribuição normal como modelo para uma característica de qualidade. Pelo teoria sabemos que se os limites de especificação estão a uma “distância” de 3 desvios padrão de cada “lado” do valor nominal, ou alvo, ela produzirá cerca de 99,73% deles com qualidade e o resto será refugo ou retrabalho.
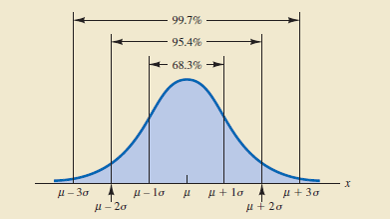
Figura 1
Em um processo seis sigma precisa “caber” 6 desvios padrão (sigmas) entre as especificações, ao invés dos 3 citados acima. Para isso o processo precisa ter menor variabilidade. Quando o conceito de processo 6 sigma foi desenvolvido na Motorola eles entenderam que mesmo em um processo considerável estável ao longo de muitos anos sua média ele ainda estará sujeito a perturbações. E tais perturbações poderão desloca-lo até 1,5 desvio padrão do seu alvo. A Figura 2 mostra essa situação.
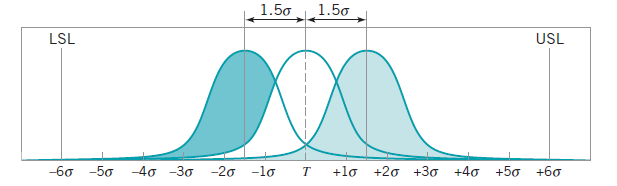
Figura 2
Assim, 6-1.5=4.5, ou seja, um processo 6 sigma é aquele onde entre o limite inferior de especificação e o superior de especificação existe 4.5 sigmas para cada lado do valor nominal, o que resulta em 3.4 PPM.
Em matemática essa afirmação ficaria P(média-4.5xDP<=X<=média+4.5DP/média=valor nominal)=3.4 PPM
Esta foi a solução dada pela Motorola, apesar da aparente inconsistência, já que só faz sentido medirmos Capabilidade de processos estáveis, ou seja, de processos que tenham a média constante.
A razão que levou a Motorola a fazer isto é que nenhum processo ou sistema é verdadeiramente estável e mesmo nas melhores situações os distúrbios ocorrem. Este distúrbios podem resultar em uma pequena mudança na média do processo, fazendo com que ela se desvio do alvo. O conceito de um processo seis sigma é uma maneira de modelar este comportamento. Como todos os modelos, ele provavelmente não é exatamente correto, mas tem se provado uma maneira útil para se pensar sobre o desempenho do processo.