Experimentos fatoriais são um conjunto de ferramentas importantíssimas usadas nos cursos de DOE, Green Belt e Black Belt. Para implementar um experimento fatorial selecionamos um número fixo de níveis de cada fator ou variáveis e então executamos algumas vezes o experimento para todas as possíveis combinações. Nesse post iremos discutir como implementar experimentos fatoriais quando temos dois níveis para 3 fatores, ou seja, um experimento 2^3, mas pode ser generalizado para um experimento com mais de 3 fatores. Ao final, mostramos um vídeo de como implementar experimentos fatoriais no Minitab.
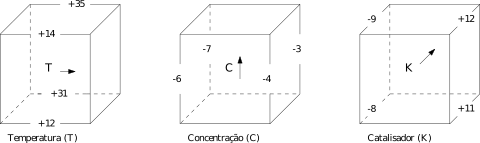
A seguir, vamos ilustrar a implementação com um exemplo de um experimento fatorial 2^3. Ou seja, temos 2 níveis para cada um dos 3 fatores, gerando 2x2x2=2^3 combinações de fatores. Os níveis serão denominados como “+” ou “-“, indicando o nível mais baixo e o nível mais alto. Abaixo temos uma imagem que exemplifica bem o experimento fatorial 2^3. Do lado esquerdo temos todas as combinações possíveis e do lado direito um cubo em que cada vértice é uma das combinações da tabela ao lado.
Figura 1: Ilustração de um experimento fatorial 2^3.
Um exemplo
Vamos utilizar um exemplo do capítulo de Delineamento Fatorial com 2 níveis do livro de planejamento de experimentos de Box, Hunter & Hunter. Suponha que você queira estudar o rendimento em % de uma solução produzida (resposta) realizando um experimento fatorial 2^3 com dois fatores quantitativos, temperatura e concentração, e uma variável qualitativa, tipo de catalisador.
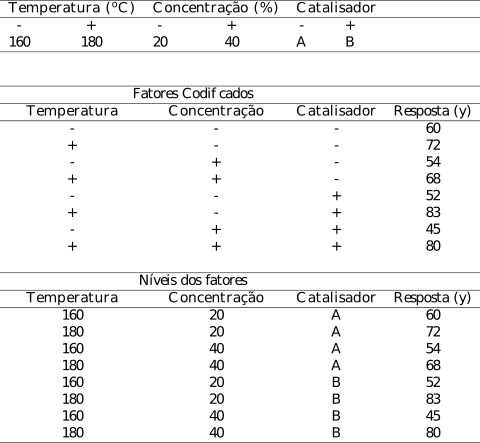
A Tabela 1 abaixo contem os valores do experimento. Na primeira tabela informa os níveis dos três fatores em questão: temperatura, concentração e tipo de catalisador. A segunda tabela mostra as combinações possíveis do planejamento ilustrada pelos sinais “+” e “-” e a resposta obtida através da média de duas replicações da configuração. Na última tabela substituímos os sinais pelos respectivos níveis e a resposta se mantem, pois nada foi alterado.
Tabela 1: Dados do experimento fatorial.
Os números da Tabela 1 podem ser ilustrados no cubo de delineamento mostrado na Figura 1. O resultado pode ser visto na Figura 2 abaixo.
Figura 2: Cubo fatorial com números do experimento exemplo acima.
Preciso mesmo desenhar esse cubo?
Não. O cubo fatorial serve apenas como ferramenta de visualização. O que você precisa mesmo é dos dados da Tabela 1 para partir para a próxima etapa: calcular os efeitos principais.
Como calcular os efeitos principais
Considere mais uma vez o exemplo ilustrado na seção anterior. Se fixarmos a concentração em 20% e a utilização do catalisador A, podemos ver produção de solução a 160 graus é de 60% e a 180 graus é de 72%. Ou seja, uma diferença de 72 – 60 = 12% passando de 160 para 180 graus, mantendo os outros fatores fixos. Note que essa diferença pode ser calculada para outras combinações de fatores fixos. A média de todas essas diferenças possíveis é denominada de efeito principal do fator. No caso da temperatura, podemos ver todos os seus efeitos e o efeito principal resultante da média desses na Tabela 2 abaixo.
Tabela 2: Efeitos da temperatura no experimento.
| Concentração | Catalisador | Produção (%)com T a 160 (T-) | Produção com T a 180 (T+) | Efeito = T+ – T- |
| 20 | A | 60 | 72 | 72 – 60 = 12 |
| 40 | A | 54 | 68 | 68 – 54 = 14 |
| 20 | B | 52 | 83 | 83 – 52 = 31 |
| 40 | B | 45 | 80 | 80 – 45 = 35 |
| Efeito principal da temperatura (média dos efeitos) | (12 + 14 + 31 + 35)/4 = 23 | |||
O mesmo cálculo pode ser reproduzido para obter os efeitos principais da concentração e tipo de catalisador. Para isso, mantenha fixos os outros fatores e calcule a diferença entre a resposta quando seu fator de interesse está no nível “+” menos a resposta com o nível do fator de interesse em “-“. Assim, podemos obter os efeitos principais dos fatores: 23 para temperatura, -5 para concentração e 1.5 para tipo de catalisador.
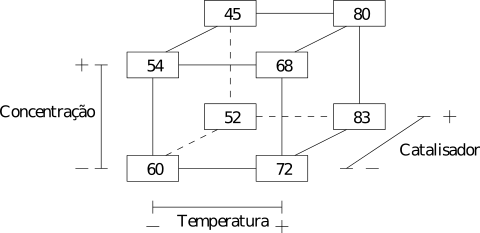
Podemos utilizar novamente o cubo fatorial para ilustrar os efeitos de cada fator. Na Figura 3 as arestas do cubo representam a diferença entre as respostas para cada uma das 4 combinações dos fatores fixados, sendo a seta no centro no cubo indicando a direção em que a diferença foi calculada.
Figura 3: Efeitos dos fatores do experimento.
Verificando se há interação entre os fatores
Note na Figura 3 que os efeitos da temperatura utilizando o catalisador do tipo B (ao fundo) é consideravelmente maior que os efeitos da temperatura utilizando o catalisador do tipo A (frente). Isso é uma evidência de que os fatores temperatura e tipo de catalisador interagem, ou seja, há interação entre os fatores.
Para obter o efeito dessa interação, basta calcular a média das 4 respostas quando os níveis são iguais (++ e –) e média das 4 respostas quando os níveis são diferentes (+- e -+). Depois isso, faça a diferença da média de níveis iguais menos a média de níveis diferentes.
Na Tabela 3 abaixo, em tons mais escuros estão as combinações de temperatura e tipo de catalisador com níveis iguais (++ e –) e de fundo branco com níveis diferentes (+- e -+). Tome a média das respostas em tom mais escuro e faça a diferença com a média das respostas de fundo branco. O resultado será (60+54+83+80)/4 – (72+68+52+45)/4 = 10. Ou seja, o efeito de interação entre temperatura de tipo de catalisador é 10. As outras interações podem ser calculadas da mesma maneira.
Tabela 3: Resultado do experimento fatorial com linhas em destaque para calcular efeito de interação.
| Temperatura | Concentração | Catalisador | Resposta (y) | ||||
| – | – | – | 60 | ||||
| + | – | – | 72 | ||||
| – | + | – | 54 | ||||
| + | + | – | 68 | ||||
| – | – | + | 52 | ||||
| + | – | + | 83 | ||||
| – | + | + | 45 | ||||
| + | + | + | 80 |
Todos esses cálculos podem ser obtidos em algum software estatístico como o Minitab. Ao final desse post disponibilizamos um link para um vídeo tutorial de como fazer todo esse processo de interações, não apenas dois a dois, mas também três a três e assim por diante.
Como interpretar os resultados
Em geral, os resultados são disponibilizados em uma tabela, como na Tabela 4, com os efeitos principais de cada fator e suas respectivas interações seguidas do erro padrão. Esse erro padrão é uma medida de precisão do efeito principal, ou seja, altos valores indicam baixa certeza acerca do valor mostrado pelo efeito principal.
Tabela 4: Efeitos e seus respectivos erros padrão calculados para o exemplo de fatorial 2^3.
| Fatores e interações | Efeito ± Erro Padrão |
| Temperatura, T | 23.0 ± 1.4 |
| Concentração, C | -5.0 ± 1.4 |
| Tipo de catalisador, K | 1.5 ± 1.4 |
| T x C | 1.5 ± 1.4 |
| T x K | 10.0 ± 1.4 |
| C x K | 0.0 ± 1.4 |
| T x C x K | 0.5 ± 1.4 |
Em meio a todos esses números, precisamos primeiro identificar o que realmente importa. Ou seja, quais efeitos são significativos. Em estatística dizemos que um efeito é significativo se temos evidências o suficiente para dizer que o valor o qual ele estima é diferente de zero. Neste caso, o efeito estimado deve ser consideravelmente maior que o seu erro padrão, caso contrário a imprecisão da estimativa não nos permite garantir que ela está estimando algo diferente de zero. Assim, baseado na teoria estatística de planejamento de experimentos, vamos considerar como significativos os efeitos que são 2.3 vezes maior que o erro padrão.
No caso do exemplo desse post, são significativos os efeitos dos fatores temperatura e concentração e a interação entre temperatura e tipo de catalisador (T x K). Porém, quando há uma interação significativa, temos que considerar os fatores envolvidos. Por exemplo, a interação T x K foi significativa, mas o tipo de catalisador tem um efeito quase igual ao seu erro padrão, mas mesmo assim vamos considerá-lo para a análise pois interage com a temperatura. Na Tabela 5 temos apenas os efeitos significativos para explicar a variabilidade da variável resposta.
Tabela 5: Efeitos significativos e seus respectivos erros padrão calculados para o exemplo de fatorial 2^3.
| Fatores e interações | Efeito ± Erro Padrão |
| Temperatura, T | 23.0 ± 1.4 |
| Concentração, C | -5.0 ± 1.4 |
| Tipo de catalisador, K | 1.5 ± 1.4 |
| T x K | 10.0 ± 1.4 |
Agora com apenas os efeitos significativos em mãos, podemos analisá-los e tirar as conclusões necessárias. Comecemos pela concentração, efeito que não possui nenhuma interação significativa com outro fator. O efeito -5 indica que cada unidade de concentração que eu aumento no meu experimento reduz em média 5 pontos percentuais do rendimento da solução (variável resposta). Ou seja, concentração possui um efeito negativo no rendimento da solução.
Analisemos agora os efeitos da temperatura e tipo de catalisador. Como há interação entre os dois fatores, não podemos analisá-los separadamente. Utilizando o catalisador do tipo A o efeito da temperatura é de 13 unidades, mas utilizando o catalisador do tipo B seu efeito aumenta para 33 unidades. Ou seja, quando utilizo o catalisador do tipo B, cada unidade de temperatura que aumentamos produz um aumento de 33 pontos percentuais no rendimento da solução.
No entanto, precisamos tomar cuidado em como tirar conclusões a partir desse experimento. O resultado obtido sobre o efeito da interação entre temperatura e tipo de catalisador é muito bom, mas não quer dizer que se eu aumentar 4 unidades de temperatura utilizando o catalisador do tipo B vou obter um rendimento de 132%. Impossível. Os resultados devem ser utilizados como um guia de onde devemos explorar mais e realizar mais estudos. Não fique satisfeito com apenas um experimento, use os resultados para planejar outro experimento agora mais específico e com o objetivo de entender melhor os fatores que são significativos.
Como implementar um experimento fatorial no Minitab?
Todos esses cálculos podem ser feitos de maneira rápida e fácil no Minitab. Clique no botão abaixo e assista a uma vídeo-aula do prof. Marcelo Petenate da Escola EDTI e aprenda a implementar experimentos fatoriais no Minitab.
Se interessou pela metodologia de experimentos fatoriais ensinados nos cursos de DOE, Green Belt e Black Belt? Confira nossos treinamentos abertos e fique a vontade para tirar suas dúvidas clicando no botão abaixo.